Digital Logic and Boolean Algebra

Introduction

We now tackle the lowest of the six levels mentioned in the introduction -- the digital logic level.

Digital:

means that we are dealing with `digits', i.e. discrete quantities as opposed to continuous or analogue quantities;

Logic:

indicates that the electronics is implementing a form of mathematics based on logic - propositional logic.

First we will introduce propositional logic - `Boolean algebra'. Then we will show how simple logic (Boolean) functions are implemented in computer hardware.

Logic

Introduction

Since at least 400 B.C. human beings have been studying what it means to think and to reason. Two closely related aims can be identified:

• To understand the process of mental reasoning.

• To develop methods to mechanise thinking and reasoning, e.g. to develop procedural methods for doing mathematical proofs, or simply to give procedures by which a thinker could come up with a rational answer to a difficult question, or, more lately, as in the study of Artificial Intelligence, to develop methods by which computers may be programmed to perform tasks that require intelligence.

Broadly speaking, logic is the study of the principles and patterns of reasoning, argument and proof. Again generalising, we can say that logic uses a language that is a formalisation of certain types of natural language statements.

You should be aware that there are two distinct but related forms of logic:

• Propositional logic - which is closely related to Boolean algebra. We will have cause to use elements of propositional logic in this course. And, you will come across it frequently in your other courses. Note: in programming, where you will have already come across statements like: if(x == 10 && y == 20) (test the truth of the logic statement x is-equal-to 10 and y is-equal-to 20.
• Predicate calculus, which is at the basis of the Prolog programming language.

Propositional Logic

Propositional logic deals with statements (propositions) which make claims which can be either true or false. Thus, valid propositions are:

• Dublin is the capital of Ireland.

• Belfast has more than 100,000 inhabitants.

• Manchester United are Premiership Champions.

• Joe Bloggs is a first year QUB student.

The test for validity is as follows: you must be able to meaningfully append to the statement "is true" (or "is false").

Thus "Dublin is the capital of Ireland is true".

Notice, however, how "Manchester United are Premiership Champions" may need time/date qualification.

The following are invalid propositions.

• What is the capital of Ireland? (a question)

• Has Dublin a large population? (a question)

• Go now to room 1.15! (a command)

• Will you come to the Botanic Inn with me on Thursday? An invitation - variations on which may be called a "proposition" in everyday language!

Generalisation/Abstraction: Symbolic Logic

We can make symbols stand-for any proposition, e.g.

$p = \text{''Dublin is the capital of Ireland''}$. Hence, in propositional calculus, the `Boolean' variable p has the truth value true.

$q = \text{''Belfast has more than 100,000 inhabitants''}$.

Compound Propositions

We can now combine elementary propositions using logic connectives to make compound or complex propositions.

Conjunction - and

Dublin is the capital of Ireland and Belfast has more than 100,000 inhabitants is true.

The combined proposition is true if-and-only-if both elements are true.

In this case, let us agree that both are true, so that the statement:

Arsenal are European Champions and Belfast has more than 100,000 inhabitants is false.

The meaning of and can be neatly summarised with a truth-table using abstract symbols:

 

Table 3.1: Truth-table for conjunction

p	q	$p\ \text{and}\ q$
F	F	F
F	T	F
T	F	F
T	T	T

 

Other symbols for conjunction are: $\wedge$ (looks like an A), and, in C/C++/Java, &&.

Disjunction - or

Note that or has two natural language meanings: exclusive-or, only one of the statements can be true at any time; inclusive-or, only either one or the other needs be to be true, or both; without any qualification, or generally means inclusive-or.

The meaning of or is given by the following truth-table:

 

Table 3.2: Truth-table for disjunction

p	q	$p\ \text{or}\ q$
F	F	F
F	T	T
T	F	T
T	T	T

 

Other symbols for disjunction: $\vee$, and, in C/C++/Java, $\mid\mid$.

Negation - not

If a proposition p is true, then not(p) is false.

The meaning of not is given by the truth-table:

 

Table 3.3: Truth-table for negation

p	$\text{not}\ q$
F	T
T	F

 

Other symbols for negation: $\neg$, $\sim$, and, in C/C++/Java, !.

A Limitation of Propositional Logic

[This section included only for completeness - not part of CSC 722.]

Let us have the proposition: Joe Bloggs is in first year and Joe Bloggs is QUB student.

And we know that the first year computing science class is in 1.15 at 9.30am on Thursdays.

Given that information, you and I can easily deduce a (relatively certain) plan on how to get in contact with Bloggs - i.e. hang about 1.15 at around that time.

But propositional logic cannot handle this problem. Let us simplify, the pattern is the same:

Socrates is a person (or Socrates is human) - a perfectly valid proposition.

All persons are mortal, i.e. they have a finite lifespan.This is not a valid proposition. It has, as we shall see, a variable hidden in it. "Socrates" is OK, but "person" can stand for any person and this is not allowed in propositional logic.

Therefore, Socrates is mortal - another valid proposition.

For this we need predicate calculus.

Predicate Calculus

[This section is included only for completeness - not part of CSC 722.]

If you had gone to primary school before about 1965, you would have leaned to parse natural language sentences into: subject, predicate. Thus, Dublin (subject) is the capital of Ireland (predicate).

In predicate calculus we restrict the meaning of predicate to possession of a property or attribute, e.g. the property of being the capital of Ireland.

Predicate calculus then allows us to handle the statement:

All persons are mortal.

as

All persons have the property of being mortal.

which, making the variable explicit, expands to:

For all persons X, X has the property of being mortal.

Another example:

Some students get up early.

Some students have the property of getting up early.

which, making the variable explicit, expands to:

For at least one student Y, Y has the property of getting up early.

or

There exists a student Y, Y has the property of getting up early.

Quantification

Universal quantification - For all $\forall$

In terms of propositional logic, universal quantification can be explained by expanding/enumerating over all the cases:

For all persons X, X has the property of being mortal.

isMortal(person1) AND isMortal(person2) AND isMortal(person3) 
AND ... up to the last person.

Since it is and, for the overall proposition to be true, all components must be true.

Existential quantification - There exists $\exists$

In terms of propositional logic, existential quantification can be explained by expanding/enumerating over all the cases:

There exists a student Y, Y has the property of getting up early.

getsUpEarly(student1) OR getsUpEarly(student2) OR getsUpEarly(student3) 
OR ...  up to the last student.

Since it is or, for the overall proposition to be true, only one component need be true.

Set Theory

The propositional calculus on truth values is equivalent to (isomorphic with) the calculus of set operations:

$$\begin{eqnarray*}\mathbf{and} &\leftrightarrow &\cap\ (\text{intersection})\\ \... ...\\ \mathbf{not} & \leftrightarrow &\sim\ (\text{complement})\\ \end{eqnarray*}$$

Digital Logic

Digital computers are constructed from switching circuits which implement propositional calculus - Boolean algebra; indeed, the term switching algebra is sometimes used. `Switch-on' might be associated with true and `off' with false. However, equally, so long as everyone is agreed as to the convention, `on' could be associated with false and `off' with true.

Likewise, the physical entities representing the values could be {voltage-low, voltage-high} or {light-off, light-on}, or whatever. Very often, we use {0, 1} - the binary digits - to represent {false, true}.

The essence of Boolean algebra is that we have only two allowable values, which we can label whatever we like, usually: {false, true}, or {0, 1}, and the two binary operations mentioned above: conjunction (and), and disjunction (or), together with the unary operation negation (not). There are other binary operations, but they can be expressed in terms of these three.

Let us now examine these operations or functions - to emphasise that they are functions, we write them in prefix notation, remarking, however, that the infix notation conveys exactly the same meaning. In addition, we use the value set {0,1}, recalling that the set {false, true} is entirely equivalent.

Conjunction - and

$$\begin{eqnarray*}\mathbf{and}(0, 0) &= &0 \\ \mathbf{and}(0, 1) &= &0 \\ \mathbf{and}(1, 0) &= &0 \\ \mathbf{and}(1, 1) &= &1 \\ \end{eqnarray*}$$

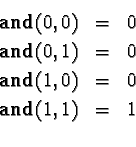
Of course, this is the same thing as Table 3.1.

Because there is a slight analogy with numerical multiplication, and is sometimes denoted by the infix `.', or just concatenation of the input variables; also, and itself is often written in infix form. Thus, for Boolean variables p, q, and r, the following are equivalent:

$$\begin{eqnarray*}r &= &\mathbf{and}(p, q)\\ r &= & p\ \mathbf{and}\ q \\ r &= & p \wedge q \\ r &= & p.q \\ r &= & pq \\ r &= & p \& q \end{eqnarray*}$$

Disjunction - or

$$\begin{eqnarray*}\mathbf{or}(0, 0) &= &0 \\ \mathbf{or}(0, 1) &= &0 \\ \mathbf{or}(1, 0) &= &0 \\ \mathbf{or}(1, 1) &= &1 \\ \end{eqnarray*}$$

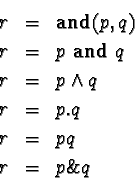
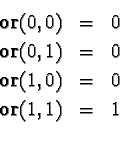
Of course, this is the same thing as Table 3.2.

Because there is a slight analogy with numerical addition, or is sometimes denoted by `+'. Thus, for Boolean variables p, q, and r, the following are equivalent:

$$\begin{eqnarray*}r &= &\mathbf{or}(p, q)\\ r &= & p\ \mathbf{or}\ q \\ r &= & p \vee q \\ r &= & p+q \\ \end{eqnarray*}$$

Negation - not

$$\begin{eqnarray*}\mathbf{not}(0) &= &1 \\ \mathbf{not}(1) &= &0 \\ \end{eqnarray*}$$

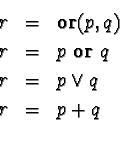
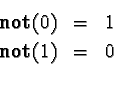
This is the same thing as Table 3.3.

Because there is a slight analogy with numerical negation, or is sometimes denoted by variations of - and $\sim$. Thus, for Boolean variables p, q, the following are equivalent:

$$\begin{eqnarray*}q &= &\mathbf{not}(p)\\ q &= & \neg p \\ q &= & \bar{p} \\ q &= & \sim p \\ q &= & p' \end{eqnarray*}$$

0, 1 are not numbers!

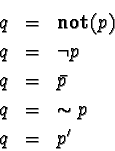
The analogies with arithmetic (and `ordinary' algebra) may cause confusion for the unwary; remember that $\{0, 1\}$ stand for $\{\text{false}, \text{true}\}$ and that it makes no sense at all to do arithmetic on them - no more sense than, for example, attempting to multiply a Java text String by, say, 25.

And, or are binary, not is unary and the associative law

Although it is not uncommon to see $p + q + r = p\ \mathbf{or}\ q\ \mathbf{or}\ r$, you must remember that both or and and are binary - meaning two parameter functions. Thus, strictly,

p + q + r = p + (q + r) = or(p, or(q, r)),

just as in Java, if(x==2||y==3||z==4) strictly could be written if(x==2||(y==3||z==4)).

Of course, in `ordinary' algebra, + and $\times$ -, etc. are also binary, but the associative law, see section 3.3.2 for these operations allows us to string a series of them together. Note: in `ordinary' algebra, there are two minuses, a unary one (-1) and a binary one (3 - 1 = 2); always remember that if you have to write an expression evaluator program.

Equivalences of Boolean Algebra

 

Just as it helps to know that in ordinary algebra, $a \times x + b \times x + a \times y + b \times y = (a + b) \times (x + y)$, or that x + (-x) = 0, it is useful to be aware of the more useful equivalences (or identities or laws) of Boolean algebra. Some of them are shown in Table 3.4. Some of these are intuitive, some not. For each equivalence there are duals - where and is swapped for or and vice-versa. For completeness, we show the table in two forms, Table 3.4, using the mathematicians $\wedge, \vee, \neg$ notation, and Table 3.5, using the engineers $., +, \bar{ }\$ notation.

 

Table 3.4: Basic equivalences of Boolean algebra - mathematics notation

Name	and dual	or dual
Identity	$1 \wedge p = p$	$0 \vee p = p$
Null	$0 \wedge p = 0$	$1 \vee p = 1$
Idempotency	$p \wedge p = p$	$p \vee p = p$
Inverse	$p \wedge \neg p = 0$	$p \vee \neg p = 1$
Commutation	$p \wedge q = q \wedge p$	$p \vee q = q \vee p$
Distribution	$p \vee (q \wedge r) = (p \vee q) \wedge (p \vee r)$	$p \wedge (q \vee r) = (p \wedge q) \vee (p \wedge r)$
Association	$p \wedge (q \wedge r) = (p \wedge q) \wedge r$	$p \vee (q \vee r) = (p \vee q) \vee r$
Absorption	$p \wedge (p \vee q) = p$	$p \vee (p \wedge q) = p$
de Morgan	$\neg (p \wedge q) = (\neg p) \vee (\neg q)$	$\neg (p \vee q) = (\neg p) \wedge (\neg q)$

 

 

Table 3.5: Basic equivalences of Boolean algebra - engineering notation

Name	and dual	or dual
Identity	$1\ . \ p = p$	0 + p = p
Null	$0 \ . \ p = 0$	1 + p = 1
Idempotency	$p \ . \ p = p$	p + p = p
Inverse	$p \ . \ \bar{p} = 0$	$p + \bar{p} = 1$
Commutation	$p \ . \ q = q \ . \ p$	p + q = q + p
Distribution	$p + (q \ . \ r) = (p + q) \ . \ (p + r)$	$p \ . \ (q + r) = (p \ . \ q) + (p \ . \ r)$
Association	$p \ . \ (q \ . \ r) = (p \ . \ q) \ . \ r$	p + (q + r) = (p + q) + r
Absorption	$p \ . \ (p + q) = p$	$p + (p \ . \ q) = p$
de Morgan	$\overline{(p \ . \ q)} = (\bar{p}) + (\bar{q})$	$\overline{(p + q)} = (\bar{p}) \ . \ (\bar{q})$

 

Truth-Tables used in Proofs

We have already shown truth-tables for and, or and not - Tables 3.1, 3.2, and 3.3. They can also be used for proving results like those above.

Example. Verify: p + p.q = p

 

Table 3.6: Truth-table proof of p + p.q = p

p	q	p.q	p	p + p.q
0	0	0	0	0
0	1	0	0	0
1	0	0	1	1
1	1	1	1	1

 

Comparison of columns 4 (p) and 5 (p + p.q) proves the result.

Exercise. Use a truth-table to prove $p + \bar{p}.q = p + q$.

How many rows in a truth-table? In the example above, we have two input variables, $p,\ q$, hence we have 2² rows - these enumerate all the possibilities of $(p,\ q)$, where $p,\ q$ can take on values from only $\{0, 1\}$.

Ex. How many rows for a truth-table involving $a,\ b,\ c$? $a,\ b,\ c,\ d$? $a,\ b,\ \bar{c}$? $a,\ b,\ c,\ \bar{c}$?

Ex. In integer arithmetic, you want to prove that x.y + (-x).y = 0. Is it possible to do this using a table? Hint: how many rows?

Logic Gates

Logic gates are the hardware implementation of logic functions. Again, all Boolean functions can be implemented using a combination of and, or, and not gates. The term gate comes from the operation of the and gate, see below, which, if one of its inputs is false, blocks or gates the other input, even if it is true.

Microprocessors, and other digital logic integrated circuits (chips) are simply massive collections of interconnected gates.

Because of a particular twist of fate in the physics of transistors - of which logic gates are constructed - it turns out that real circuits tend to employ nand and nor gates a good deal in preference to and and or:

nand:

$p\ \mathbf{nand}\ q = \mathbf{not}(p\ \mathbf{and}\ q)$

nor:

$p\ \mathbf{nor}\ q = \mathbf{not}(p\ \mathbf{or}\ q)$

[A good many of the figures in the remainder of this chapter are from [Tanenbaum, 1999], chapter 3].

Transistor implementations

For completeness, we show transistor implementations of not (also called an inverter), nand and nor. Again for completeness, we give the following model of a transistor when it is operated in so-called switching mode.

Transistor as a Switch

There are three connections - collector, base, and emitter. The positive power supply (e.g. +5 volts) is applied to the collector via a resistor; the emitter (the one with the arrow) is connected to ground/earth. The input signal is applied to the base. When the input signal is high, say > 3 volts when the power is 5 volts, the transistor switches on, i.e. current is allowed to flow down to the emitter and out to ground. When the input signal is low, the transistor switches off i.e. little or no current is allowed to flow.

The net effect of the transistor in Figure 3.1(a) switching on is that the output is connected to ground and V_out takes the voltage of ground - $\sim 0$ volts. Thus high input (V_in) - logic 1 - yields low output - logic 0; thus, not, inversion.

The net effect of the transistor switching off is that the output takes on the voltage $\sim V_{cc}$ volts. Thus low input (V_in) - logic 0 - yields high output - logic 1; thus, not, inversion.

With this model in mind, it is easy to verify that the circuits in Figures 3.1(b) and (c) do in fact operate as nand and nor.

  

Figure 3.1: (a) Not (b) nand (c) nor

If you would like to see mechanical implementations of gates (levers, also water valves), see [Hillis, 1999].

Symbols for Logic Gates

Figure 3.2 shows the symbols, and truth-tables, for the five basic logic gates.

  

Figure 3.2: Symbols and truth-tables for (a) not (b) nand (c) nor (d) and (e) or

The circles denote negation - not, inversion. It is possible to have negation on inputs too.

Logic Circuit Analysis

There are two fairly distinct activities in working with digital logic, analysis, and synthesis.

Analysis:

given a circuit, what does it do? i.e. what Boolean function does it implement.

Synthesis:

given a Boolean expression, produce a circuit that implements it - preferably using a minimal number of gates. This is synthesis or design.

This section covers analysis.

Example. What does the circuit in Figure 3.3 do?

  

Figure 3.3: Truth-table (a) and circuit (b) for majority of three circuit

It takes a majority vote over the three inputs.

Exercise. Verify the truth-table in Figure 3.3(a) by creating an expanded truth table containing columns for $A, B, C, \bar{A}, \bar{B}, \bar{C}, \bar{A}BC, A\bar{B}C, AB\bar{C}, ABC$. Note: starting from scratch, and not knowing the answer, this is the way you would normally do it - you cannot hope to work out column M in your head.

Equivalent Circuits

Quite often, because of a preference for nand, nor, or because there are spare gates left over, it may be desired to implement and, or, and not using nand, nor. Figure 3.4 shows some examples.

  

Figure 3.4: (a) not, (b) and, and (c) or functions implemented using nands and nors

Let us examine the nand gate (top) in Figure 3.4(a).

$\overline{A.A} = \overline{A},\ \text{since, from the idempotency law}\ A.A = A$.

Now the nand version (top) of Figure 3.4(b): the input to the second gate is clearly $\overline{AB}$, and we already know that, connected like this, the second nand gate performs negation, and two negations cancel, hence AB.

Exercise. Use Boolean algebra to verify that the two circuits in Figure 3.4(c), do, in fact, perform or.

Exclusive-or

 

Exclusive-or, commonly abbreviated to xor, as opposed to inclusive-or, see the discussion above, captures the meaning either one or the other, but not both - i.e. it outputs a 1 if the inputs are different. We will have cause to refer to it later, so it is worthwhile to show a circuit - Figure  3.5 shows three possible circuits and a truth-table. Figure  3.5(b) directly implements the Boolean expression most usually associated with xor: $\bar{A}B + A\bar{B}$.

  

Figure 3.5: Exclusive or - three implementations

Generations of Integrated Circuits

Integrated circuits started to appear in the late 1960s. A typical single chip of that age - but still available to buy today - is shown in Figure  3.6; it contains four nand gates and has 14 pins.

  

Figure 3.6: Integrated circuit containing just four nand gates

Nowadays, an integrated circuit such as Figure  3.6 is said to be small scale integrated (SSI). Small scale integrated circuits contain up to 10 gates (up to about 100 transistors). In the late 1960s, complete computers were made from SSI; still, this was a lot better than the individual devices (transistors, resistors, etc.) of the 1950s and 60s. And, a fantastic improvement over the vacuum tubes used in the 1940s.

You will still find SSI circuits, e.g. Transistor-transistor-logic (TTL) 74xx00 quad 2-input nand used on the periphery of computer systems, and as the `glue' which connects the more complex circuits/chips together.

In SSI chips, as many gates of a given type as possible are put in the package (chip). The number of gates is limited by the number of pins, and to a lesser extent by the ability to dissipate the heat generated by the circuit. On the 74xx00 you have: power 2 pins + 4 x (2 inputs + 1 output) = 3 for each NAND gate = total of 14 pins. An additional consideration is the area taken up by such an SSI chip, roughly $2.5 cm \times 1 cm$.

In the case of early TTL each chip would consume about 10 milliWatts of power.

Later medium scale integrated (MSI) circuits began to appear - containing 10-100 gates. Later on large scale integrated (LSI) containing 100-100,000 gates. The first microprocessors (1971 - the 4 bit Intel 4004) would have been classified LSI. Now we have very large scale integrated (VLSI), and beyond. The latest Pentium III contains in the region of 10,000,000 transistors.

A great many very complex complete components are now available on single chips - microprocessors, disk controllers, modems, .... On the other hand, there is still a need to design circuits from simple gates. But, building large circuits from SSI is simply impractical - it would take too much space and consume too much power. Hence, programmable logic arrays (PLAs) and field programmable gate arrays (FPGAs).

Programmable Logic Arrays

A programmable logic array contains a large array of not, and gates and or gates on a single chip. The user can connect certain gates by breaking certain (fuse) connections. Figure 3.7 contains an example.

  

Figure 3.7: A programmable logic array. The squares represent fuses which can be blown to disable connections, and so determine which function is implemented, i.e. programmed

Exercises

1.

(Section 3.3) Us a truth-table to verify the or version of de Morgan's Law: $\overline{(p + q)} = (\bar{p}) \ . \ (\bar{q})$

2.

Use de Morgan's law to find the complement of $p\bar{q}$.

3.

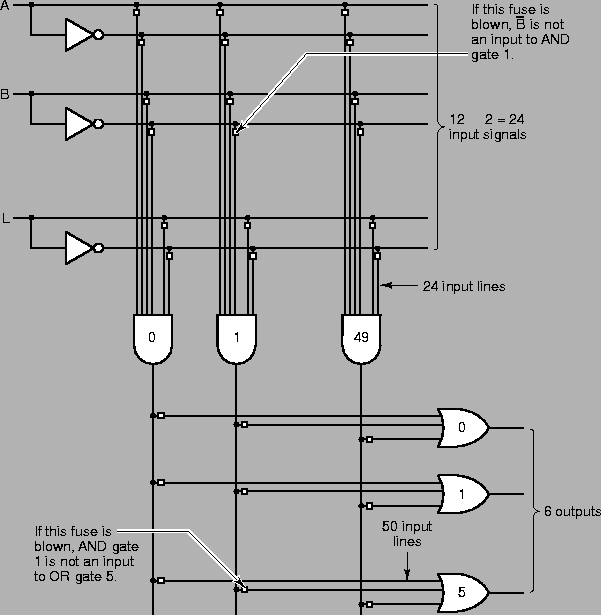(a) Explain how de Morgan's law can be made to simplify (or at least make it more understandable) the following Java if statement:

     int i;
     if( (i<=2) || (i>=5) )System.out.println(i);

(b) Explain, in plain English, the circumstances under which the 'THEN' part gets executed, and i gets printed.

(c) Explain how de Morgan's law can be made to simplify (or at least make it more understandable) the following Java if statement:

     if( (i>12) || ( !(i<20) ) )System.out.println(i);

(d) Explain, in plain English, the circumstances under which the 'THEN' part gets executed, and i gets printed.

4.

(a) Explain how de Morgan's law can be made to simplify (or at least make it more understandable, or show the nonsense of!) the following Java if statement, as before int i;:

     if( !(i<=92) || !(i>=100) )System.out.println(i);

(b) Explain, in plain English, the circumstances under which the 'THEN' part gets executed, and i gets printed.

5.

Use a truth-table to verify the inverse law: $p + \bar{p} = 1$.

6.

Prove that $pq + p\bar{q} = p$ Hint: use the or form of the inverse law: $p + \bar{p} = 1$.

7.

Verify the truth of the compound statement Manchester United are European Champions or they are World Club Champions.

8.

Verify the truth of the compound statement it is not the case that Manchester United are European Champions and World Club Champions.

9.

Verify the middle row of Figure 3.4 -- and and or implemented using nand gates; i.e. express Boolean algebra and prove.

10.

Simplify the following using Boolean algebra: (a) $\bar{A}\bar{B} + AB + \bar{A}B$; (b) $AB\bar{C} + ABC + A\bar{B}\bar{C} + A\bar{B}C$.

11.

Simplify the following, explaining your steps: (a) 0.1; (b) 0+1; (c) (1.1).(1+0); (d) (1+1).A; (e) $\bar{A}.(A+B)$; (f) A.(A+B'); (g) A xor A; (h) $A \mathbf{xor} \bar{A}$.

Note the error in the caption of Figure 3.5; it should read "Exclusive or".

12.

See Figure 3.5 (a); discuss how xor relates to equivalence/equality.

13.

How would you use two xors, two inverter/nots, and an and to create a circuit to compare two two-bit numbers; Hint: see Figure 4.8.

14.

Is it possible to make an xor gate using just nand gates? - if possible write the equation.

15.

Look back at Chapter 2 and the rules for binary addition; assume that you are adding bits a, b. Create a truth table for a, b, sum; compare with xor. Create a truth table for a, b, carry; compare with the truth-table for and.

16.

See pages 55-57. Consider the task of making a Pentium III microprocessor out of 7400 chips (Figure 3.6). I reckon you can get about $100 \times 7400$ chips onto a card the size of a PC motherboard, and about 25 of those cards into a cabinet the size of a filing cabinet, and I could get 100 filing cabinets into my room; how many rooms for your Pentium III?

What will be the power consumption?

17.

The following equation describes a two-input multiplexer: when A is false the output is (the same as) D₀, when A is true the output is (the same as) D₁: $D_0.\bar{A} + D_1.A$. (a) Verify this statement using a truth table.

(b) Draw a diagram for a two-input multiplexer -- see Figure 4.1.

(c) A four input multiplexer will have four inputs -- and one output; how many control lines (A, B, C, ...); again, see Figure 4.1.

(d) Sketch a diagram for a four-input multiplexer.

18.

Draw a diagram of a two-input multiplexer that uses on/off switches.

19.

Show how you would construct a 2-to-1 multiplexer using a 7400 quad NAND gate (Figure 3.6) -- concentrate on the fact that it has 4 NAND gates.

20.

Create a truth-table to verify that the following circuit performs the action of a two-to-one multiplexer. Compare F with Y and Z, and see what happened for S(witch) = 0, S = 1.

               Y-------------------NAND
                                   NANDo-----+
                    +-------NOTo---NAND      |
                    |                        +---NAND
                    |                            NANDo--- F
                    |                        +---NAND
                    +--------------NAND      |
                    |              NANDo-----+
               Z-------------------NAND
                    |
                    S
[Note:         |
          -----+------  these lines are connected
               |
          ------------  these lines are NOT connected]
               |

21.

Verify that the following circuit computes a majority decision over A, B, C, i.e. for (A, B, C) = (1, 0, 0), the output is 0, whilst for (0, 1, 1) or 1, 1, 1 etc. the output is 1. A is connected to AND gates 1 and 2, B is connected to AND gates 1 and 3, and C is connected to AND gates 2 and 3.

               A-----------+--------AND
                           |        AND------+
                    +---------------AND      |
                    |      |                 |
                    |      +--------AND      +--OR
               B----+               AND----------OR--- F
                    |      +--------AND      +--OR
                    |      |                 |
                    +---------------AND      |
                           |        AND------+
               C-----------+--------AND

22.

A single input decoder (see Figure 4.2 for a 3 input decoder) takes one input (say A) and has two outputs D₀, D₁; for A = true, D₁ = 1, and D₀ = 0; A = false, vice-versa; (a) Give the equations for D₀, D₁; (b) Based on Figure 4.2, draw a diagram of a 1-to-2 decoder.