CSC722 Examination April 2000

[B1.] Boolean Algebra, Number Systems, Computer System Components

(a)

Verify the following Boolean relation:

$\bar{A}B C + A \bar{B}C + A B \bar{C}+ A B C = A B + A C + B C$

(i)

algebraically; if you wish, refer to Appendix 2;

(ii)

using a truth-table.

[5marks]

(b)

Assuming eight-bit twos complement signed representation, perform the following arithmetic computations in binary. In each case, supplement your answer with conversions of both operands, and the result, to decimal; moreover, indicate whether your result is valid or invalid, and, if invalid, give a clear indication why.

(i)               (ii)              (iii)
    1000 0110         1000 0111          1000 1111    
   +0000 0101        +1111 1110         +1000 0000
    ---------         ---------          ---------

[6marks]

(c)

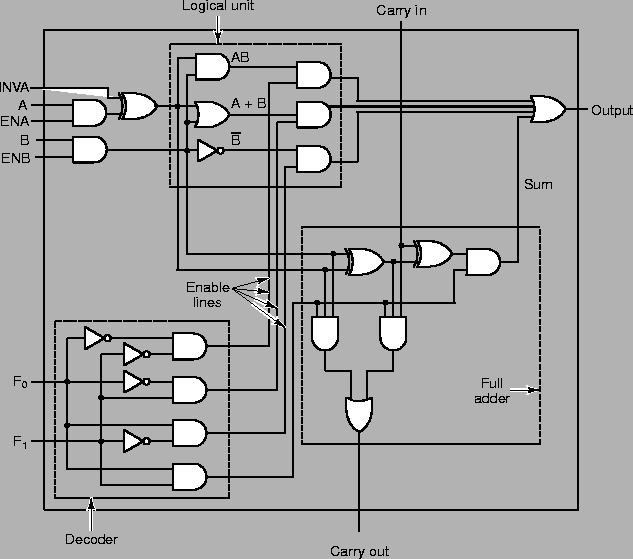
Figure A.1 shows a one bit ALU.

(i)

Explain the purpose of F₀, F₁.

[2marks]

(ii)

Paying attention to the decoder section, describe precisely the outputs on each enable line (refer to them as E₀, E₁, E₂, E₃, reading from the top), for each possible input of F₀, F₁.

[4marks]

(iii)

Show how eight of one-bit ALUs may be combined to produce an eight bit ALU.

[3marks]

  

Figure A.1: A one bit ALU

[B2.] Assembly Language Programming and the Assembly Process

(a)

The following example shows an implementation of an IF ...THEN ...ELSE construct in Mac-1 assembly language.

L0:       LODD a0
          SUBD a1
          JPOS L2
          JZER L2
L1:       LOCO 1 
          STOD a2
          JUMP L3
L2:       LOCO 0
          STOD a2
L3:     ...

(i)

Determine the contents of the IF condition, and the THEN and ELSE parts of the program and describe it using Java or suitable pseudo-code.

[2marks]

(ii)

Add comments to each line of the assembly code, to explain how the assembly language performs the task, and replace the labels L0, L1, L2, L3 with more explanatory labels (e.g. IF, THEN, ELSE, ...).

[4marks]

(b)

Referring to Appendix 1.1, manually assemble the Mac-1 assembly code given in (a); give brief explanations of any significant steps. Assemble the program to start at location 100Hex; you may assume that the variables a0, a1, ..., a10 will be at addresses 500Hex, 501Hex, ...50AHex.

[10marks]

(c)

Explain, with the aid of examples, the memory addressing modes: immediate, direct, and indirect.

[4marks]

[B3.] Input-Output, and Subprogam Handling

(a)

The following describes a simple memory mapped input-output scheme used by Mac-1:

Mac-1a uses memory-mapped input-output, wherby some memory cells are mapped to input-output ports; for simplicity we assume that there are only two ports, one connected to a standard-input device, another connected to a standard-output device.

Input: data port is mapped to 4092/FFCHex (lower-order byte = data byte); status port is mapped to 4093/FFDHex, when the sign bit (most significant bit) is set, this denotes data available.

Output: data port is mapped to 4094/FFEHex (lower-order byte); status 4095/FFFHex; sign bit set denotes ready ...

Briefly, explain the principle used in both read and write operations.

[3marks]

(b)

Write a program fragment which will, paying proper attention to ready status, write the contents of the lower- order byte of address 500 to the output device mentioned in part (a).

[4marks]

(c)

Referring to Appendix 1.2, explain the operation of the Mac-1 instructions: call and retn; you should mention the roles of the stack and stack pointer; illustrate your answer with appropriate examples / diagrams. In your answer please mention the major reasons why call and retn cannot be replaced by simple jump instructions.

[7marks]

(d)

Write a Mac-1 subprogram to find the maximum of two integers, i.e. in Java-like syntax:

          int max(int x, int y)
          {
            if (x > y) return x;
            else return y;
          }

and the call: c = max(a, b);

Pay particular attention to: (i) in the calling program, how to pass the two arguments via the stack, and how to call the subprogram; (ii) in subprogram max itself, how to access the two parameters x, y. Hint: lodl, and subl - for the comparison.

[6marks]

Appendix 1.1, Mac-1a Instruction Set - limited version of Mac-1, with machine code

   -------------------------------------------------------------------
   Binary         Mnemonic  Name                    Action(s)
   ------         --------  ----                    ---------
  --------------------------------------------------------------------
  0000XXXXXXXXXXXX  lodd   Load Direct            ac <- m[x]
  0001XXXXXXXXXXXX  stod   Store Direct           m[x] <- ac
  0010XXXXXXXXXXXX  addd   Add Direct             ac<- ac + m[x]
  0011XXXXXXXXXXXX  subd   Subtract Direct        ac <- ac - m[x]
  0100XXXXXXXXXXXX  jpos   Jump on pos.         IF ac>=0 : pc <- x
  0101XXXXXXXXXXXX  jzer   Jump on zero         IF ac=0 : pc <- x
  0110XXXXXXXXXXXX  jump   Jump uncond.         pc <- x (0 <= x <=4095)
  0111CCCCCCCCCCCC  loco   Load constant        ac <- c (0 <= c <=4095)
  --------------------------------------------------------------------

Appendix 1.2, Complete Mac-1 Instruction Set

Mnemonic  Name                Action(s)
--------  ----                ---------
lodd x    Load Direct         ac <- m[x]
stod x    Store Direct        m[x] <- ac
addd x    Add Direct          ac<- ac + m[x]
subd x    Sub. Direct         ac <- ac - m[x]
jpos x    Jump on pos.        IF ac>=0 : pc <- x
jzer x    Jump on zero        IF ac=0 : pc <- x
jump x    Jump uncond.        pc <- x (0 <= x <=4095)
loco c    Load constant       ac <- c (0<=c<=4095)
lodl x    Load local          ac <- m[sp+x]
stol x    Store local         m[sp+x] <- ac
addl x    Add local           ac <- ac + m[sp+x]
subl x    Subtract local      ac <- ac - m[sp+x]
jneg x    Jump on negative    if ac<0 : pc <- x
jnze x    Jump on nonzero     if ac!=0 : pc <- x
call x    Call procedure      sp<-sp-1; m[sp] <- pc; pc <- x
pshi      Push indirect       sp <- sp-1; m[sp]<-m[ac]
popi      Pop indirect        m[ac] <- m[sp]; sp <- sp+1
push      Push onto stack     sp <- sp-1; m[sp] <- ac
pop       Pop off stack       ac <- m[sp]; sp <- sp+1
retn      Return from proc.   pc <- m[sp]; sp <- sp + 1
swap      Swap ac, pc         temp <- ac; ac <- sp; sp<-temp
insp y    Increment sp        sp <- sp + y; (0 <= y <= 255)
desp y    Decrement sp        sp <- sp - y; (0 <= y <= 255)

Notes:  1. c is a constant in range 0 - 4095
        2. x is an address in range 0 - 4095
        3. y is an address offset in range 0 - 255

Appendix 2, Equivalences of Boolean Algebra

 

Table A.1: Basic equivalences of Boolean algebra -- engineering notation

Name	and dual	or dual
Identity	$1\ . \ p = p$	0 + p = p
Null	$0 \ . \ p = 0$	1 + p = 1
Idempotence	$p \ . \ p = p$	p + p = p
Inverse	$p \ . \ \bar{p} = 0$	$p + \bar{p} = 1$
Commutation	$p \ . \ q = q \ . \ p$	p + q = q + p
Distribution	$p + (q \ . \ r) = (p + q) \ . \ (p + r)$	$p \ . \ (q + r) = (p \ . \ q) + (p \ . \ r)$
Association	$p \ . \ (q \ . \ r) = (p \ . \ q) \ . \ r$	p + (q + r) = (p + q) + r
Absorption	$p \ . \ (p + q) = p$	$p + (p \ . \ q) = p$
de Morgan	$\overline{(p \ . \ q)} = (\bar{p}) + (\bar{q})$	$\overline{(p + q)} = (\bar{p}) \ . \ (\bar{q})$