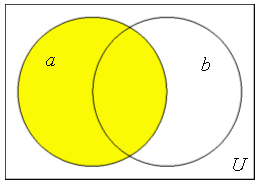

The Venn diagram is a graphical way to represent sets and set operations. Each diagram begins with a rectangle illustrating the universal set. Then each set is represented by the interior of a circle, square, or other shape.
Below are Venn diagrams for the set a, shaded in yellow, and for the complement of a, everything in U that is not in a.
 | 
|
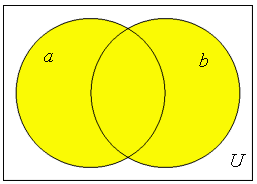
| Venn diagram for set a | Venn diagram for set a' |
 | 
|
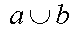 | 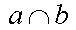
|
The inhibition operations "a, but not b" and "b, but not a" are clearly not commutative, as shown by their Venn diagrams below
 | 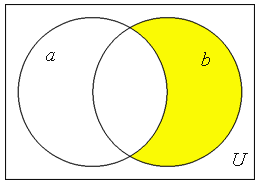
|
 | 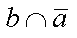
|
The exclusive or operation, "a or b, but not both", is clearly commutative from the symmetry of its Venn diagram.

|
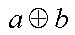
|
A Venn diagram ideally should have a separate region for each minterm. For n variables, there are 2n minterms. They are typically listed in a truth table.
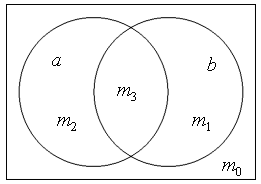 |
| |||||||||||||||
| Venn diagram regions | truth table |
Maintained by John Loomis, last updated 30 May 2004