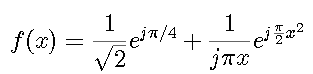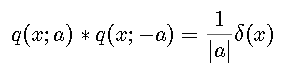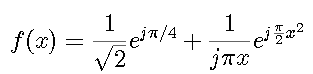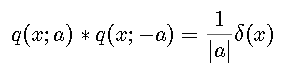EOP513 Fourier Optics Assignment 5
- Do problems 4-1 through 4-4 from the textbook.
- The following approximation to the Fresnel integral function is
valid for large x.
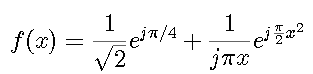
Find an appropriate lower-limit for x (1% error). Use Matlab to plot the
real and imaginary parts of the Fresnel integral and the approxmation function.
- Do problems 4-7, 4-9, and 4-10 as follows.
Set the aperture geometry using appropriate Matlab
functions. Generate an image of the input. Use Matlab
to find the Fraunhofer pattern. (See fdiffract.m)
Generate an image of the output. Use appropriate image
scaling to show the shape of the diffraction pattern.
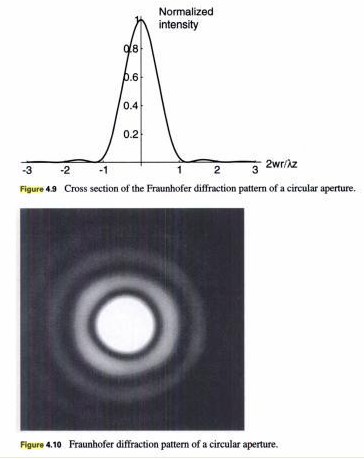
- Generate the diffraction pattern of a circular
aperture (normalized radius w = 1). Use Matlab to find
the Fraunhofer pattern (using method in fdiffract.m.
Show both input and output images. Try to scale the image to
approximate the appearance of Fig 4.10 in the textbook.
Plot a radial cross-section
of the output. Superimpose on this plot, the Airy pattern computed
from Eq. 4-31 in the textbook (generated using somb2(x), see
somb.m).
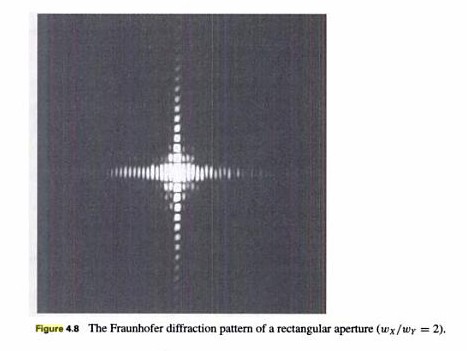
- Generate the diffraction pattern of a rectangular aperture
(wx/wy = 2). Try to scale the image (size
and irradiance) to approximate the appearance of Fig 4.8 in the
textbook.
- Show that
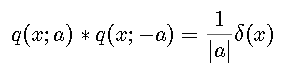
- Generate the following aperture functions using cyl.m,
rect.m, and polygon.m. Find the Fraunhofer pattern and
show both your input and output images.


Maintained by John
Loomis, last updated 9 June 2009